1 Manipulando pixels em uma imagem
Manipular pixels em uma imagem envolve a capacidade de alterar individualmente os elementos de cor que compõem a imagem. Cada pixel contém informações sobre sua cor específica, como vermelho, verde e azul (RGB), além de valores de transparência em alguns casos. Ao manipular os pixels, é possível realizar uma variedade de transformações na imagem, como ajustar o brilho, a saturação, o contraste, aplicar filtros, redimensionar ou recortar. Essas manipulações permitem corrigir imperfeições, realçar detalhes, criar efeitos especiais, entre outras possibilidades. A manipulação de pixels é uma técnica fundamental em áreas como processamento de imagem, design gráfico, edição de fotos e criação de arte digital. Com a ajuda de bibliotecas de processamento de imagem, é possível acessar e modificar os valores dos pixels em uma imagem, abrindo caminho para inúmeras possibilidades criativas e práticas.
1.1 Exercicio 1.1 - Filtro Negativo (regions.cpp)
O filtro negativo é um mecanismo que busca eliminar conteúdos indesejados, inapropriados ou prejudiciais por meio da aplicação de técnicas de análise e restrição. Ele é amplamente utilizado em diversas áreas, como tecnologia da informação, mídias sociais e segurança, visando proteger os usuários e garantir a qualidade do conteúdo. No entanto, é necessário ter cautela para evitar restrições excessivas e preservar a liberdade de expressão.
Com isso, crie um programa chamado regions com base no código de exemplo "pixels.cpp". O programa deve pedir ao usuário as coordenadas de dois pontos, P1 e P2, que estão dentro dos limites do tamanho da imagem. Em seguida, ele deve exibir a imagem fornecida, mas com a região definida pelo retângulo formado pelos pontos P1 e P2 exibindo o negativo da imagem nessa área específica. Esse efeito produzirá uma região destacada com cores invertidas em relação ao restante da imagem.
1.1.1 Código e Resultado.
// Renato Emanuel Medeiros de Lira
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main(int, char** argv) {
Mat image;
image=imread(argv[1], IMREAD_GRAYSCALE);
if (image.empty()) {
cout << "Imagem não foi carregada" << endl;
return 1;
}
Point p1, p2;
cout << "Tamanho da imagem: " << image.rows << "x" << image.cols << endl;
cout << "Digite as coordenadas do ponto P1:" << endl;
cin >> p1.y >> p1.x;
do{
cout << "Digite as coordenadas do ponto P2:" << endl;
cin >> p2.y >> p2.x;
if (p1.y >= p2.y || p1.x >= p2.x){
cout << "Ambas coordenadas do ponto P2 tem que ser maiores que as coordenadas do ponto P1, escreva novamente!"<<endl;
}
}while(p1.y >= p2.y || p1.x >= p2.x);
for (int i = p1.x; i < p2.x; i++) {
for (int j = p1.y; j < p2.y; j++) {
image.at<uchar>(i, j) = 255 - image.at<uchar>(i, j);
}
}
namedWindow("janela", WINDOW_AUTOSIZE);
imshow("janela", image);
waitKey(0);
imwrite("Regions.png", image);
return 0;
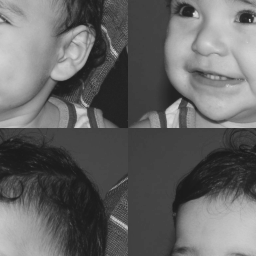
}Abaixo temos a imagem original biel e em seguida a imagem resultante do código regions. As Coordenadas escolhidas foram P1 (90, 180) e P2 (90, 180).


1.2 Exercicio 1.2 - Troca Regiões (trocaregioes.cpp)
Desenvolva um programa chamado trocaregioes com base no código de exemplo "pixels.cpp". O programa deve trocar os quadrantes diagonais na imagem. Para realizar essa troca, utilize a classe "Mat" e seus construtores para criar as regiões que serão intercambiadas. Ao executar o programa, a imagem exibida terá os quadrantes diagonais trocados.
1.1.2 Código e Resultado.
// Renato Emanuel Medeiros de Lira
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main(int, char** argv) {
Mat image;
image=imread(argv[1], IMREAD_GRAYSCALE);
if (image.empty()) {
cout << "Imagem não foi carregada" << endl;
return 1;
}
int x = image.rows;
int y = image.cols;
Mat temp = image.clone();
Rect region1(0, 0, y/2, x/2);
Rect region2(y/2, 0, y/2, x/2);
Rect region3(0, x/2, y/2, x/2);
Rect region4(y/2, x/2, y/2, x/2);
Mat roi1 = temp(region1);
Mat roi2 = temp(region2);
Mat roi3 = temp(region3);
Mat roi4 = temp(region4);
roi3.copyTo(image(region2)); // R3 -> R2
roi4.copyTo(image(region1)); // R4 -> R1
roi1.copyTo(image(region4)); // R1 -> R4
roi2.copyTo(image(region3)); // R2 -> R3
imshow("janela", image);
waitKey(0);
imwrite("trocaregioes.png", image);
return 0;
}Abaixo temos a imagem original biel e em seguida a imagem resultante do código trocaregioes, na qual os quadrantes foram trocados de lugar.
2 Serialização de dados em ponto flutuante via FileStorage
A serialização de dados em ponto flutuante usando o FileStorage envolve a gravação e leitura de valores numéricos em formato de ponto flutuante em um arquivo estruturado. Ao utilizar a classe FileStorage, é possível gravar os dados em um formato como YAML ou XML, permitindo a preservação da precisão fracionária. A leitura dos dados serializados também é facilitada pela classe FileStorage, tornando possível acessar e utilizar os valores gravados posteriormente. Esse processo é especialmente útil em cenários onde é necessário armazenar e recuperar informações numéricas precisas, como em aplicações científicas, processamento de imagens e simulações.
2.1 Exercicio 2 - filestorage.cpp
Utilizando o programa "filestorage.cpp" como base, crie um novo programa que gere uma imagem de 256x256 pixels contendo uma senóide horizontal com 4 períodos e amplitude de 127, semelhante à figura apresentada na filestorage. Grave a imagem em formato PNG e em formato YML. Em seguida, compare os arquivos gerados, extraindo uma linha de cada imagem gravada e calculando a diferença entre elas. Trace um gráfico dessa diferença ao longo da linha correspondente nas imagens. Observe os resultados e faça as observações relevantes.

2.1.1 Código e Resultado.
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
int side = 256;
int periodos = 4;
Mat image(side, side, CV_8UC1);
for (int i = 0; i < side; i++) {
for (int j = 0; j < side; j++) {
float value = 127 * sin(2 * CV_PI * periodos * j / side) + 128;
image.at<uchar>(i, j) = static_cast<uchar>(value);
}
}
string filenameYML = "senoide.yml";
string filenamePNG = "senoide.png";
FileStorage fs(filenameYML, FileStorage::WRITE);
fs << "mat" << image;
fs.release();
imwrite(filenamePNG, image);
FileStorage fs_read(filenameYML, FileStorage::READ);
fs_read["mat"] >> image;
fs_read.release();
imshow("image", image);
waitKey();
return 0;
}Abaixo temos a imagem resultante do código filestorage, na qual é representado uma senoide horizontal com 4 periodos e amplitude de 127. A imagem é semelhante a figura filestorage usada como exemplo.

3 Decomposição de imagens em planos de bits
A decomposição de imagens em planos de bits é um processo onde uma imagem é separada em camadas binárias, cada uma representando um plano de bits específico. Isso permite analisar e manipular individualmente cada componente da imagem, seja em escala de cinza ou em cores, como vermelho, verde e azul. Essa técnica é útil em diversas aplicações, como processamento de imagem, análise de padrões e compressão de dados, possibilitando identificar características específicas e realizar manipulações precisas na intensidade de cor de cada pixel.
3.1 Exercicio 3 - esteg-encode.cpp
Escreva um programa que seja capaz de recuperar uma imagem codificada resultante de esteganografia. No processo de recuperação, os bits menos significativos dos pixels da imagem fornecida devem ser utilizados para compor os bits mais significativos dos pixels da imagem recuperada. O programa deve receber como parâmetro de linha de comando o nome do arquivo da imagem resultante da esteganografia
3.1.1 Código e Resultado.
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main(int argc, char** argv) {
Mat imagemCodificada, imagemEscondida, imagemPortadora, imagemDecodificada;
Vec3b valCod, valEsc, valPort, valDec;
int nbits = 5;
// Recebendo a imagem codificada;
imagemCodificada = cv::imread(argv[1], cv::IMREAD_COLOR);
if (imagemCodificada.empty()) {
cout << "Imagem nao carregou corretamente" << endl;
return -1;
}
// Inicializando as matrizes clonadas
imagemEscondida = Mat(imagemCodificada.size(), imagemCodificada.type());
imagemPortadora = Mat(imagemCodificada.size(), imagemCodificada.type());
imagemDecodificada = Mat(imagemCodificada.size(), imagemCodificada.type());
// Realizando a decodificação da imagem;
for (int i = 0; i < imagemCodificada.rows; i++) {
for (int j = 0; j < imagemCodificada.cols; j++) {
valCod = imagemCodificada.at<Vec3b>(i, j);
valEsc[0] = valCod[0] << nbits;
valEsc[1] = valCod[1] << nbits;
valEsc[2] = valCod[2] << nbits;
imagemEscondida.at<Vec3b>(i, j) = valEsc;
valPort[0] = valCod[0] >> nbits << nbits;
valPort[1] = valCod[1] >> nbits << nbits;
valPort[2] = valCod[2] >> nbits << nbits;
imagemPortadora.at<Vec3b>(i, j) = valPort;
valDec[0] = valCod[0] >> (8 - nbits) << (8 - nbits);
valDec[1] = valCod[1] >> (8 - nbits) << (8 - nbits);
valDec[2] = valCod[2] >> (8 - nbits) << (8 - nbits);
imagemDecodificada.at<Vec3b>(i, j) = valDec;
}
}
imwrite("imagemEscondida.png", imagemEscondida);
imwrite("imagemPortadora.png", imagemPortadora);
imwrite("imagemDecodificada.png", imagemDecodificada);
return 0;
}Esse programa recupera a imagem codificada a partir dos bits menos significativos dos pixels da imagem esteganografada fornecida. Os bits 6 e 7 dos canais de cor de cada pixel são zerados para compor os bits mais significativos da imagem recuperada. Abaixo temos a imagem Decodificada imagemDecodificada, a imagem escondida imagemEscondida e a imagem portadora imagemPortadora, todas sendo saída do código esteg.



4 Preenchendo regiões
Uma tarefa comum em processamento de imagens e visão computacional é contar a quantidade de objetos em uma cena. Para isso, é necessário identificar os aglomerados de pixels associados a cada objeto. Geralmente, trabalha-se com imagens binárias, em que cada pixel tem o valor 0 para o fundo da imagem e 255 para os objetos. Cada aglomerado de pixels é considerado um objeto separado, e esse processo é amplamente utilizado para contagem de objetos em imagens.
4.1 Exercicio 4 - labeling.cpp
O programa "labeling.cpp" apresenta uma limitação quando há mais de 255 objetos na cena devido à utilização de pixels de 8 bits para rotular os objetos. Para solucionar esse problema, é necessário utilizar uma estrutura de dados com maior capacidade de armazenamento, como uma matriz de inteiros de 32 bits. Além disso, é possível aprimorar o algoritmo de contagem para identificar regiões com ou sem buracos internos, removendo os objetos que tocam as bordas da imagem e contando separadamente os buracos internos de cada objeto identificado.
4.1.1 Código e Resultado.
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace cv;
void removeBordas(Mat& image) {
int width = image.cols;
int height = image.rows;
// Remover objetos das bordas
for (int i = 0; i < width; i++) {
floodFill(image, Point(i, 0), 255);
floodFill(image, Point(i, height - 1), 255);
}
for (int i = 0; i < height; i++) {
floodFill(image, Point(0, i), 255);
floodFill(image, Point(width - 1, i), 255);
}
}
void contarObjetos(Mat& image, int& nObjects, int& nBuracos) {
int width = image.cols;
int height = image.rows;
nObjects = 0;
nBuracos = 0;
// Alterar o background
floodFill(image, Point(0, 0), 100);
// Contar objetos e buracos
for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
if (image.at<uchar>(i, j) == 0) {
// Contar buraco
nBuracos++;
floodFill(image, Point(j, i), nBuracos);
} else if (image.at<uchar>(i, j) == 255) {
// Contar objeto
nObjects++;
floodFill(image, Point(j, i), 200);
}
}
}
}
int main(int argc, char** argv) {
Mat image = imread(argv[1], IMREAD_GRAYSCALE);
if (!image.data) {
std::cout << "Imagem nao carregou corretamente\n";
return -1;
}
removeBordas(image);
int nObjects, nBuracos;
contarObjetos(image, nObjects, nBuracos);
std::cout << "A figura tem " << nObjects << " bolhas\n";
std::cout << "A figura tem " << nBuracos << " buracos\n";
imshow("image", image);
imwrite("labeling.png", image);
waitKey();
return 0;
}O código labeling está contando certo o número de bolhas com buracos, mas parece que houve um problema na lógica utilizada para identificar as bolhas sem buracos. A abordagem utilizada não está correta e acabou removendo todas as bolhas sem buracos da imagem. Na imagem labeling, podemos ver melhor o que aconteceu

5 Manipulação de histogramas
5.1 Exercicio 5 - histogram.cpp
5.1.1 Código e Resultado.
6 Filtragem no domínio espacial
Um filtro espacial é uma técnica utilizada no processamento de imagens para modificar a aparência de uma imagem por meio da aplicação de uma máscara ou kernel sobre seus pixels. Essa máscara é usada para realizar operações de convolução, que combinam os valores dos pixels vizinhos para calcular um novo valor para cada pixel da imagem, permitindo realces, suavização, detecção de bordas e outras transformações visuais.
6.1 Exercicio 6 - filtroespacial.cpp
Utilizando o programa exemplo filtroespacial.cpp como referência, implemente um programa laplgauss.cpp. O programa deverá acrescentar mais uma funcionalidade ao exemplo fornecido, permitindo que seja calculado o laplaciano do gaussiano das imagens capturadas. Compare o resultado desse filtro com a simples aplicação do filtro laplaciano.
6.1.1 Código e Resultado.
#include <iostream>
#include <opencv2/opencv.hpp>
void printmask(cv::Mat& m);
void applyFilters(cv::Mat& frame, cv::Mat& result, const cv::Mat& mask, bool absolut);
int main(int argc, char** argv) {
if (argc != 2) {
std::cout << "Uso: " << argv[0] << " <caminho_para_imagem>\n";
return -1;
}
cv::Mat frame = cv::imread(argv[1]);
if (frame.empty()) {
std::cout << "Imagem não encontrada ou não pode ser lida\n";
return -1;
}
float media[] = {0.1111, 0.1111, 0.1111, 0.1111, 0.1111,
0.1111, 0.1111, 0.1111, 0.1111};
float gauss[] = {0.0625, 0.125, 0.0625, 0.125, 0.25,
0.125, 0.0625, 0.125, 0.0625};
float horizontal[] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
float vertical[] = {-1, -2, -1, 0, 0, 0, 1, 2, 1};
float laplacian[] = {0, -1, 0, -1, 4, -1, 0, -1, 0};
float laplacianOfGaussian[] = {0.0625, 0.125, 0.0625, 0.125, 0.25,
0.125, 0.0625, 0.125, 0.0625, -1, -1, -1, -1, -8, -1, -1, -1, -1};
cv::Mat mask(3, 3, CV_32F);
cv::Mat result, resultLoG;
int absolut = 1; // calcs abs of the image
char key = 0;
cv::namedWindow("filtroespacial", cv::WINDOW_NORMAL);
cv::namedWindow("original", cv::WINDOW_NORMAL);
mask = cv::Mat(3, 3, CV_32F, media);
while (key != 27) {
applyFilters(frame, result, mask, absolut);
cv::GaussianBlur(result, resultLoG, cv::Size(3, 3), 0);
cv::Laplacian(resultLoG, resultLoG, CV_8U, 3, 1, 0, cv::BORDER_DEFAULT);
cv::imshow("original", frame);
cv::imshow("filtroespacial", result);
cv::imshow("laplacian_of_gaussian", resultLoG);
cv::imwrite("original.png", frame);
cv::imwrite("filtroespacial.png", result);
cv::imwrite("laplacian_of_gaussian.png", resultLoG);
key = (char)cv::waitKey(10);
switch (key) {
case 'a':
absolut = !absolut;
break;
case 'm':
mask = cv::Mat(3, 3, CV_32F, media);
printmask(mask);
break;
case 'g':
mask = cv::Mat(3, 3, CV_32F, gauss);
printmask(mask);
break;
case 'h':
mask = cv::Mat(3, 3, CV_32F, horizontal);
printmask(mask);
break;
case 'v':
mask = cv::Mat(3, 3, CV_32F, vertical);
printmask(mask);
break;
case 'l':
mask = cv::Mat(3, 3, CV_32F, laplacian);
printmask(mask);
break;
case 'b':
mask = cv::Mat(3, 3, CV_32F, laplacianOfGaussian);
printmask(mask);
break;
default:
break;
}
}
return 0;
}
void printmask(cv::Mat& m) {
for (int i = 0; i < m.size().height; i++) {
for (int j = 0; j < m.size().width; j++) {
std::cout << m.at<float>(i, j) << ",";
}
std::cout << "\n";
}
}
void applyFilters(cv::Mat& frame, cv::Mat& result, const cv::Mat& mask, bool absolut) {
cv::Mat framegray, frame32f, frameFiltered;
cv::cvtColor(frame, framegray, cv::COLOR_BGR2GRAY);
framegray.convertTo(frame32f, CV_32F);
cv::filter2D(frame32f, frameFiltered, frame32f.depth(), mask, cv::Point(1, 1), 0);
if (absolut) {
frameFiltered = cv::abs(frameFiltered);
}
frameFiltered.convertTo(result, CV_8U);
}No código filtroespacial, calculamos o filtro espacial da imagem passada como parametro, além de calcular o laplaciano do gaussiano dessa imagem. O resultado da aplicação do filtro espacial é observado na imagem filtroespacial. Já a aplicação do laplaciano do gaussiano da imagem, pode ser visto na imagem laplacian_of_gaussian


7 A Tranformada Discreta de Fourier
A transformada discreta de Fourier (DFT) é uma técnica matemática amplamente utilizada para analisar e processar sinais no domínio da frequência. Ela converte um sinal discreto no domínio do tempo em suas componentes de frequência correspondentes, permitindo a identificação e a manipulação das diferentes frequências presentes no sinal. A DFT divide o sinal em uma série de componentes senoidais complexas, cada uma representando uma frequência específica. Essas componentes são então combinadas para reconstruir o sinal original. A DFT possui aplicações em várias áreas, incluindo processamento de imagens, compressão de dados, análise espectral e filtragem de sinais, proporcionando uma ferramenta poderosa para a análise e a modificação de sinais e imagens no domínio da frequência.
7.1. Exercicio 7 - dftimage.cpp
Utilizando os programa exemplo dftimage.cpp, calcule e apresente o espectro de magnitude da imagem filestorage.
7.1.1. Código e Resultado.
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
void swapQuadrants(cv::Mat& image) {
cv::Mat tmp, A, B, C, D;
// se a imagem tiver tamanho ímpar, recorta a região para o maior
// tamanho par possível (-2 = 1111...1110)
image = image(cv::Rect(0, 0, image.cols & -2, image.rows & -2));
int centerX = image.cols / 2;
int centerY = image.rows / 2;
// rearranja os quadrantes da transformada de Fourier de forma que
// a origem fique no centro da imagem
// A B -> D C
// C D B A
A = image(cv::Rect(0, 0, centerX, centerY));
B = image(cv::Rect(centerX, 0, centerX, centerY));
C = image(cv::Rect(0, centerY, centerX, centerY));
D = image(cv::Rect(centerX, centerY, centerX, centerY));
// swap quadrants (Top-Left with Bottom-Right)
A.copyTo(tmp);
D.copyTo(A);
tmp.copyTo(D);
// swap quadrant (Top-Right with Bottom-Left)
C.copyTo(tmp);
B.copyTo(C);
tmp.copyTo(B);
}
int main() {
cv::FileStorage fs("senoide.yml", cv::FileStorage::READ);
if (!fs.isOpened()) {
std::cout << "Erro ao abrir arquivo YAML." << std::endl;
return EXIT_FAILURE;
}
cv::Mat image;
fs["image"] >> image;
if (image.empty()) {
std::cout << "Erro ao carregar a imagem." << std::endl;
return EXIT_FAILURE;
}
fs.release();
cv::Mat padded, complexImage;
std::vector<cv::Mat> planos;
// expande a imagem de entrada para o melhor tamanho no qual a DFT pode ser
// executada, preenchendo com zeros a lateral inferior direita.
int dft_M = cv::getOptimalDFTSize(image.rows);
int dft_N = cv::getOptimalDFTSize(image.cols);
cv::copyMakeBorder(image, padded, 0, dft_M - image.rows, 0, dft_N - image.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));
// prepara a matriz complexa para ser preenchida
// primeiro a parte real, contendo a imagem de entrada
planos.push_back(cv::Mat_<float>(padded));
// depois a parte imaginária com valores nulos
planos.push_back(cv::Mat::zeros(padded.size(), CV_32F));
// combina os planos em uma única estrutura de dados complexa
cv::merge(planos, complexImage);
// calcula a DFT
cv::dft(complexImage, complexImage);
swapQuadrants(complexImage);
// planos[0] : Re(DFT(image))
// planos[1] : Im(DFT(image))
cv::split(complexImage, planos);
// calcula o espectro de magnitude e de fase (em radianos)
cv::Mat magn, fase;
cv::cartToPolar(planos[0], planos[1], magn, fase, false);
cv::normalize(fase, fase, 0, 1, cv::NORM_MINMAX);
// caso deseje apenas o espectro de magnitude da DFT, use:
cv::magnitude(planos[0], planos[1], magn);
// some uma constante para evitar log(0)
// log(1 + sqrt(Re(DFT(image))^2 + Im(DFT(image))^2))
magn += cv::Scalar::all(1);
// calcula o logaritmo da magnitude para exibir
// com compressão de faixa dinâmica
cv::log(magn, magn);
cv::normalize(magn, magn, 0, 1, cv::NORM_MINMAX);
// exibe as imagens processadas
cv::imshow("Imagem", image);
cv::imshow("Espectro de magnitude", magn);
cv::imshow("Espectro de fase", fase);
cv::waitKey(0);
return EXIT_SUCCESS;
}Nesse código dftimage, não foi possivel obter o resultado pedido no exercicio, isso se pode dar devido a algum erro de lógica e/ou do uso de alguma função da biblioteca opencv.
8. Detecção de bordas com o algoritmo de Canny
O algoritmo de Canny é amplamente utilizado para detecção de bordas em imagens. Ele consiste em vários passos para identificar e caracterizar as bordas de forma precisa e robusta. Primeiramente, é aplicado um filtro gaussiano para reduzir o ruído na imagem. Em seguida, são calculados os gradientes de intensidade, fornecendo informações sobre as mudanças de intensidade em diferentes direções. Esses gradientes são então suprimidos para obter bordas mais finas e precisas. Por fim, é realizada uma técnica chamada de limiarização dupla, na qual são definidos limiares mínimos e máximos para determinar quais bordas são consideradas relevantes. As bordas resultantes são rastreadas e conectadas para formar linhas contínuas. O algoritmo de Canny é conhecido por sua capacidade de detectar bordas com baixo ruído e alta precisão, tornando-o uma escolha popular em aplicações de visão computacional e processamento de imagens.
8.1. Exercicio 8 - cannypoints.cpp
Utilizando os programas exemplos/canny.cpp e exemplos/pontilhismo.cpp como referência, implemente um programa cannypoints.cpp. A idéia é usar as bordas produzidas pelo algoritmo de Canny para melhorar a qualidade da imagem pontilhista gerada. A forma como a informação de borda será usada é livre. Entretanto, são apresentadas algumas sugestões de técnicas que poderiam ser utilizadas:
8.1.1. Código e Resultado.
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <fstream>
#include <iomanip>
#include <iostream>
#include <numeric>
#include <opencv2/opencv.hpp>
#include <vector>
#define STEP 5
#define JITTER 3
#define RAIO 3
int main(int argc, char** argv) {
std::vector<int> yrange;
std::vector<int> xrange;
cv::Mat image, frame, points, border;
int width, height, gray;
int x, y;
image = cv::imread(argv[1], cv::IMREAD_GRAYSCALE);
std::srand(std::time(0));
if (image.empty()) {
std::cout << "Could not open or find the image" << std::endl;
return -1;
}
width = image.cols;
height = image.rows;
xrange.resize(height / STEP);
yrange.resize(width / STEP);
std::iota(xrange.begin(), xrange.end(), 0);
std::iota(yrange.begin(), yrange.end(), 0);
for (uint i = 0; i < xrange.size(); i++) {
xrange[i] = xrange[i] * STEP + STEP / 2;
}
for (uint i = 0; i < yrange.size(); i++) {
yrange[i] = yrange[i] * STEP + STEP / 2;
}
points = cv::Mat(height, width, CV_8U, cv::Scalar(255));
border = cv::Mat(height, width, CV_8U);
cv::Canny(image, border, 50, 150); // Aplicar o algoritmo de Canny para detectar bordas
std::random_shuffle(xrange.begin(), xrange.end());
for (auto i : xrange) {
std::random_shuffle(yrange.begin(), yrange.end());
for (auto j : yrange) {
x = i + std::rand() % (2 * JITTER) - JITTER + 1;
y = j + std::rand() % (2 * JITTER) - JITTER + 1;
gray = image.at<uchar>(x, y);
// Verificar se o pixel é uma borda antes de desenhar o ponto
if (border.at<uchar>(x, y) > 0) {
cv::circle(points, cv::Point(y, x), RAIO, CV_RGB(gray, gray, gray),
cv::FILLED, cv::LINE_AA);
}
}
}
imshow("janela", points);
cv::waitKey(0);
cv::imwrite("pontos_canny.jpg", points); // Salvar a imagem pontilhista resultante
return 0;
}O código cannypoints apresenta uma melhoria na técnica de pontilhismo e, usando em conjunto com o algoritimo de canny, foi possivel desenhar pontos na borda do rosto presente na imagem biel. Na imagem pontos_canny, podemos ver o rosto sendo desenhado por pontos.
